Particle Transport in Steady-State Flow Field
Skip ahead to run the model
Introduction
The two-dimensional model ParticleFlow simulates flow in a rectangular domain. A key purpose of the ParticleFlow model is to illustrate how heterogeneities in hydraulic properties cause the spatial spreading of fluid particles. This spreading is analogous to macro-scale solute dispersion.
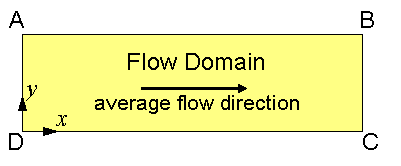
The rectangular flow domain (see above figure) is assumed to be bounded on the left and right sides (AD and BC) by specified head boundaries, and on the top and bottom (AB and DC) by no-flow boundaries. Assuming that the head along AD is higher then the head along BC, the average flow is from left to right.
Governing Equation
The steady-state ground-water flow equation to be solved is
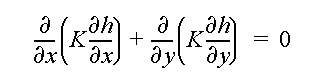
where h is hydraulic head, and K is hydraulic conductivity (assumed isotropic), and x and y are the Cartesian coordinates.
Boundary Conditions
The boundary condition along AD is
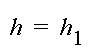
where h1 is a constant. The boundary condition along BC is
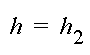
where h2 is also a constant. The boundary condition along AB and DC is
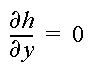
The computer model ParticleFlow solves the above equations by the finite element method. The flow domain is represented by a rectangular mesh composed of square cells, each is divided into two triangular elements. Linear basis functions are used in the finite element formulation. After solving for hydraulic head h, the x and z components of the average interstitial velocity vector are computed by
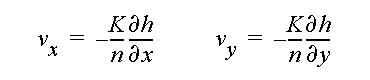
where n is porosity. The velocity vectors are used for calculating flow paths and the advective movement of fluid particles.
In a flow field with nonuniform velocity, a cloud of fluid particles will tend to spread. This spreading can be described by the spatial variance (in the x and y directions) of particle positions, defined as:
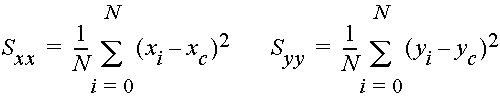
where N is the total number of fluid particles, xi and yi are the x and y coordinates of the i-th particle, and xc and yc denote the x and y positions of the center of mass, defined as
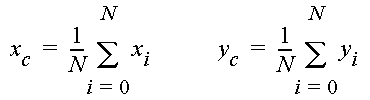
If each fluid particle is assumed to carry a fixed amount of solute mass, then particle spreading is analogous to macro-scale solute dispersion. In the macro-dispersion approach, the small-scale variation of velocity is not explicitly simulation. Instead, solute spreading is characterized by a dispersion tensor. The dispersion process is called Fickean if the plot of the spatial variances Sxx and Syy versus time show straight-line relations. In this case, the components of the dispersion coefficients can be estimated by

Running the Model
Running the model involves 5 steps. To begin each step, click the corresponding button at the top of the window. A dialog box appears for you to enter the necessary input data. The three buttons on the second row allow you to zoom in, zoom out, and quit the model.

Step 1: Start -- Specify model dimension
Step 2: Properties -- Specify hydraulic conductivity and porosity
Step 3: Head -- Compute hydraulic head
After hydraulic head is computed, two options are available. You may proceed to
Step 4a: Flow (Path) -- Track flow paths from selected
points
Step 5a: Animation -- Animate the evolution of flow
paths
or
Step 4b: Flow (Particle) -- Set up initial distribution
of fluid particles
Step 5b: Animation -- Animate the advective movement
of fluid particles